7 algorytmów, które powinien znać każdy programista

Jako student programowania prawdopodobnie nauczyłeś się wielu różnych algorytmów w trakcie swojej kariery. Biegłość w posługiwaniu się różnymi algorytmami jest absolutnie niezbędna każdemu programiście.

Przy tak wielu algorytmach śledzenie tego, co najważniejsze, może być trudne. Jeśli przygotowujesz się do rozmowy kwalifikacyjnej lub po prostu odświeżysz swoje umiejętności, ta lista ułatwi to zadanie. Czytaj dalej, ponieważ wymieniamy najważniejsze algorytmy dla programistów.

1. Algorytm Dijkstry

Edsger Dijkstra był jednym z najbardziej wpływowych informatyków swoich czasów i przyczynił się do: wiele różnych dziedzin informatyki, w tym systemy operacyjne, budowa kompilatorów i wiele jeszcze. Jednym z najbardziej godnych uwagi wkładów Dijkstry jest pomysłowość jego algorytmu najkrótszej ścieżki dla grafów, znanego również jako algorytm najkrótszej ścieżki Dijkstry.

Algorytm Dijkstry znajduje pojedynczą najkrótszą ścieżkę w grafie od źródła do wszystkich wierzchołków grafu. W każdej iteracji algorytmu dodawany jest wierzchołek z minimalną odległością od źródła i taki, który nie istnieje w bieżącej najkrótszej ścieżce. Jest to właściwość chciwości wykorzystywana przez algorytm Djikstry.

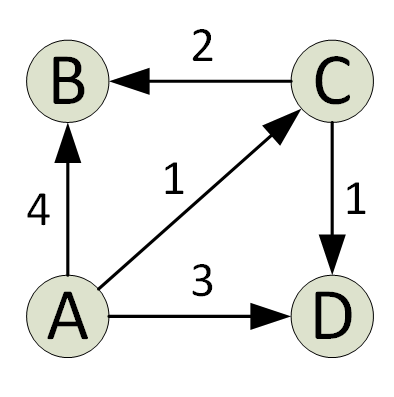
Algorytm jest zazwyczaj implementowany za pomocą zestawu. Algorytm Dijkstry jest bardzo wydajny, gdy jest zaimplementowany ze stertą min; możesz znaleźć najkrótszą ścieżkę w czasie O(V+ElogV) (V to liczba wierzchołków, a E to liczba krawędzi w danym grafie).

Algorytm Dijkstry ma swoje ograniczenia; działa tylko na grafach skierowanych i nieskierowanych z krawędziami o dodatniej wadze. W przypadku wag ujemnych zazwyczaj preferowany jest algorytm Bellmana-Forda.

Pytania do rozmowy kwalifikacyjnej często zawierają algorytm Djikstry, dlatego zdecydowanie zalecamy zrozumienie jego skomplikowanych szczegółów i zastosowań.

2. Połącz Sortuj

Na tej liście mamy kilka algorytmów sortowania, a sortowanie przez scalanie jest jednym z najważniejszych algorytmów. Jest to wydajny algorytm sortowania oparty na technice programowania Dziel i zwyciężaj. W najgorszym przypadku sortowanie przez scalanie może posortować „n” liczb w czasie tylko O(nlogn). W porównaniu z prymitywnymi technikami sortowania, takimi jak Sortowanie bąbelkowe (co zajmuje O(n^2) czasu), sortowanie przez scalanie jest bardzo wydajne.

Związane z: Wprowadzenie do algorytmu sortowania przez scalanie

W sortowaniu przez scalanie tablica do sortowania jest wielokrotnie dzielona na podtablice, aż każda podtablica składa się z jednej liczby. Algorytm rekurencyjny następnie wielokrotnie scala podtablice i sortuje tablicę.

3. Szybkie sortowanie

Quicksort to kolejny algorytm sortowania oparty na technice programowania Dziel i zwyciężaj. W tym algorytmie element jest najpierw wybierany jako element obrotowy, a następnie cała tablica jest dzielona wokół tego elementu obrotowego.

Jak zapewne zgadłeś, dobry obrót ma kluczowe znaczenie dla wydajnego sortowania. Element osiowy może być elementem losowym, elementem media, pierwszym lub nawet ostatnim elementem.

Implementacje quicksort często różnią się sposobem wyboru elementu pivot. W przeciętnym przypadku quicksort posortuje dużą tablicę z dobrym przechyleniem w czasie tylko O(nlogn).

Ogólny pseudokod quicksort wielokrotnie dzieli tablicę na element przestawny i umieszcza ją we właściwej pozycji podtablicy. Umieszcza również elementy mniejsze niż oś po lewej stronie i elementy większe niż oś po prawej stronie.

4. Głębokość pierwszego wyszukiwania

Depth First Search (DFS) to jeden z pierwszych algorytmów grafowych, których uczono studentów. DFS to wydajny algorytm używany do przeglądania lub przeszukiwania grafu. Można go również zmodyfikować, aby można go było używać podczas przechodzenia przez drzewa.

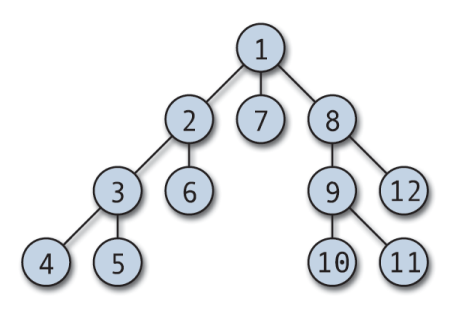
Przechodzenie DFS może rozpocząć się od dowolnego dowolnego węzła i zanurza się w każdym sąsiednim wierzchołku. Algorytm cofa się, gdy nie ma nieodwiedzonego wierzchołka lub jest ślepy zaułek. System DFS jest zwykle implementowany ze stosem i tablicą logiczną do śledzenia odwiedzanych węzłów. DFS jest prosty we wdrożeniu i wyjątkowo wydajny; to działa (V+E), gdzie V to liczba wierzchołków, a E to liczba krawędzi.

Typowe zastosowania przechodzenia DFS obejmują sortowanie topologiczne, wykrywanie cykli na wykresie, odnajdywanie ścieżek i znajdowanie silnie połączonych komponentów.

5. Wyszukiwanie wszerz

Breadth-First Search (BFS) jest również znane jako przechodzenie przez poziom dla drzew. BFS działa w O(V+E) podobnie do algorytmu DFS. Jednak BFS używa kolejki zamiast stosu. DFS zanurza się w grafie, podczas gdy BFS porusza się po grafie wszerz.

Algorytm BFS wykorzystuje kolejkę do śledzenia wierzchołków. Nieodwiedzone sąsiednie wierzchołki są odwiedzane, oznaczane i umieszczane w kolejce. Jeśli wierzchołek nie ma żadnego sąsiedniego wierzchołka, wierzchołek jest usuwany z kolejki i eksplorowany.

BFS jest powszechnie używany w sieciach peer-to-peer, najkrótszej ścieżce grafu nieważonego i do znajdowania minimalnego drzewa opinającego.

6. Wyszukiwanie binarne

Wyszukiwanie binarne to prosty algorytm do znalezienia wymaganego elementu w posortowanej tablicy. Działa poprzez wielokrotne dzielenie tablicy na pół. Jeśli wymagany element jest mniejszy niż środkowy element, lewa strona środkowego elementu jest dalej przetwarzana; w przeciwnym razie prawa strona jest dzielona na pół i ponownie przeszukiwana. Proces jest powtarzany aż do znalezienia wymaganego elementu.

Najgorsza złożoność czasowa wyszukiwania binarnego wynosi O(logn), co czyni go bardzo wydajnym w przeszukiwaniu tablic liniowych.

7. Minimalne algorytmy drzewa opinającego

Minimalne drzewo opinające (MST) grafu ma minimalny koszt spośród wszystkich możliwych drzew opinających. Koszt drzewa opinającego zależy od wagi jego krawędzi. Należy zauważyć, że może istnieć więcej niż jedno minimalne drzewo opinające. Istnieją dwa główne algorytmy MST, a mianowicie Kruskala i Prima.

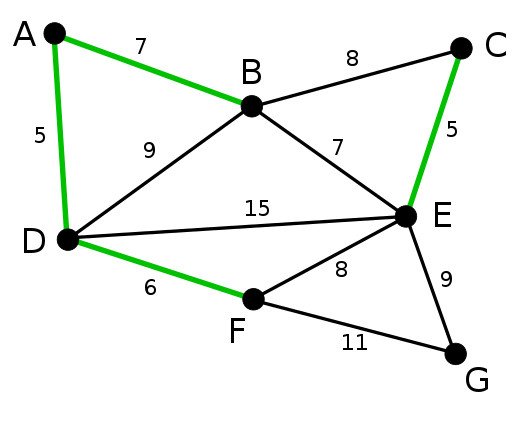
Algorytm Kruskala tworzy MST, dodając krawędź o minimalnym koszcie do rosnącego zestawu. Algorytm najpierw sortuje krawędzie według ich wagi, a następnie dodaje krawędzie do MST, zaczynając od minimum.

Należy zauważyć, że algorytm nie dodaje krawędzi tworzących cykl. Algorytm Kruskala jest preferowany dla rzadkich grafów.

Algorytm Prima wykorzystuje również właściwość zachłanności i jest idealny do gęstych wykresów. Główną ideą w MST Prima jest posiadanie dwóch odrębnych zestawów wierzchołków; jeden zestaw zawiera rosnący MST, podczas gdy drugi zawiera nieużywane wierzchołki. W każdej iteracji wybierana jest minimalna krawędź wagi, która połączy dwa zestawy.

Algorytmy minimalnego drzewa opinającego są niezbędne do analizy klastrów, taksonomii i sieci rozgłoszeniowych.

Sprawny programista biegle posługuje się algorytmami

Programiści nieustannie uczą się i rozwijają swoje umiejętności, a każdy musi znać kilka podstawowych zasad. Doświadczony programista zna różne algorytmy, zalety i wady każdego z nich oraz zna, który algorytm byłby najbardziej odpowiedni dla danego scenariusza.

Wprowadzenie do algorytmu sortowania powłok

Chociaż sortowanie według powłoki nie jest najskuteczniejszą metodą, początkujący mogą wiele zyskać na jej praktykowaniu.

Czytaj dalej

O autorze